Answer: A quadrilateral with one pair of parallel sides is called a trapezoid. Thus, this polygon with four sides is a closed form and a planar figure. There are four internal angles and four lines segments in it. A trapezoid has two bases, which are the parallel sides; its legs are the other two sides.
A trapezoid’s area can be calculated using the formula A = ½(b1+b2) h, where h is the height and b1 and b2 are the bases’ lengths. A standard trapezoid can be divided into simpler forms to determine its height and complete your computation if all you know are its side lengths.
The Trapezoid Area Theorem
We partition the polygon into triangles and compute the area of each triangle to obtain an arbitrary polygon area. The area of the polygon is equal to the sum of the areas of these triangles. This method allows us to establish a formula for the area spare of the trapezoid.
Let’s agree to refer to a trapezoid’s height as a perpendicular that is drawn from any point on one base to a straight line that includes another base. The BH line segment is the ABCD trapezoid height, as seen in the following figure:
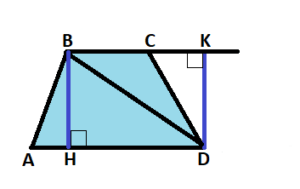
The following theorem follows from this: “The area of a trapezoid is equal to the product of the half-sum of its bases and the height.” This theorem is proven using the area formula.
The given trapezoid is: BH is height, and ABCD, AD, and BC are the base lengths.
Demonstrate that S = ½ (AD + BC) · BH is the area of this trapezoid ABCD.
Proof: Create a diagonal BD. It creates the two triangles ABD and BCD from the trapezoid. This indicates that a trapezoid ABCD’s perimeter will be equal to the total area of these triangles.
A triangle is formed by AD as the base and BH as the height. BC is the base of a triangle with the formula BCD.
It’s time to mark DK’s height. Whereas area S of triangle BCD = 1/2 BC · DK, area S of triangle ABD = 1/2 AD. BH. The area S of the triangle BCD is equal to 1/2 BC · BH since BH = DK. Therefore, 1/2 AD · BH + 1/2 BC · BH = 1/2 (AD + BC) · BH is the area S of the trapezium ABCD.
Area of Trapezoid: Formula
If we know the length of a trapezoid’s parallel sides and the height (distance) between them, we can calculate its area. The area of a trapezoid can be calculated using the following formula:
A = ½ (a + b) h
where (A) is the area of a trapezoid, ‘a’ and ‘b’ are the bases (parallel sides), and ‘h’ is the height (the perpendicular distance between a and b)
Area of Trapezoid: Solved Examples
Example 1: Determine the length of the other base of a trapezoid if its height is 12 units, area is 108 square units, and one of its bases is equal to 8 units.
Solution: ‘a’ = 8 units is one of the bases.
Let ‘b’ be the other base.
The trapezoid has an area of A = 108 square units.
It stands 12 units tall (‘h’).
Enter each of these values in the trapezoid formula’s area.
A = ½ (a + b) h
108 = ½ (8 + b) × (12)
108 = 6 (8 + b)
dividing by 6 on both sides
18 = 8 + b
b = 10
The length of the other base of the given trapezoid = 10 units.
Example 2: Determine the area of a trapezoid whose height is provided as 5 units and whose bases are given as 7 and 9 units.
Solution: For a trapezoid with a = 7, b = 9, and h = 5, its area is equal to ½ (a + b) h)
These values can be substituted into the formula to get:
A = ½ (a + b) h
A = ½ (7 + 9) × 5
A = ½ × 16 × 5 = 40 unit2
As a result, the trapezoid has an area of 40 square units.