Answer: Shapes, which you usually cover in your geometry classes are what form objects. View this pyramid, this ice cream cone, this traffic cone, this triangle ruler, and this slice of pizza. What connections do they share? Yes, it is correct. Each one of them is a triangle.
How does a triangle become a triangle? It is described as a three-line polygon with non-linear parts that intersect. Vertices are the points that connect two or more lines or curves. The angles, or the gaps between two intersecting lines, are found close to the vertex.
Now, that you know what is triangle, let’s come to the point and discuss about acute scalene triangle.
What is an Acute Scalene Triangle?
A triangle with three distinct sides and angle measurements with angles less than 90 degrees is known as an acute scalene triangle. The following characteristics define an acute scalene triangle:
- Three sharp angles
- Every side is not equal
- Three line segments that overlap
- The measures of each angle vary.
Both the acute and scalene triangle features are displayed by an acute scalene triangle. If the three sides and angles of a triangle have different measurements, the triangle is called a scalene triangle. An acute triangle is one in which all three angles are acute (less than 90 degrees).
The Identification of an Acute Scalene Triangle
You should be able to classify this type of triangle using a protractor as a measuring instrument if you keep in mind the characteristics of an acute scalene triangle.
How to Measure Angles with a Protractor?
A protractor is an instrument for measuring angles and curves. With the assistance of this instrument, you can determine whether a triangle is an acute scalene triangle by measuring its angles. The simple ways to do this are listed below:
- The vertex of the angle should be the midway (middle point) of the protractor.
- Align the opposite side with the protractor’s “zero” line.
- Follow the degrees at which the other side of the protractor crosses the numerical scale.
- After adding up all the angles, start determining if the triangle represents an acute scalene.
An acute scalene triangle would exist if
- Not all of the angles are 90 degrees or more.
- There is inequality on all sides.
What is Perimeter of Acute Scalene Triangle?
P = (a + b + c) units is the perimeter of an acute scalene triangle, which is defined as the sum of the three sides. Here, a, b, and c represent the triangle’s sides. It indicates the total length needed to create an acute triangle with scalene. We draw or create an acute scalene triangle using a rope, thread, pencil, etc., using the perimeter.
Formulas for Acute Scalene Triangles
We can swiftly determine the area and perimeter of the triangle with the use of the Scalene-Acute Triangle Formula. Let’s examine these formulas in more detail.
The area of an acute scalene triangle is expressed as Area = (1/2) × b Õ h.
In this case, “b” stands for the triangle’s base and “h” for its height.
Note: Heron’s formula, which is provided below, can be used to efficiently compute the area of an acute scalene triangle if all of its sides are known.
Using Heron’s formula, the area of an acute scalene triangle is =
√S (S−a) (S−b) (S−c) square units.
Here, a, b, and c represent the triangle’s sides, while S stands for the semiperimeter, which may be computed as S = (a + b + c)/2.
Acute Scalene Triangle: Examples and Solutions
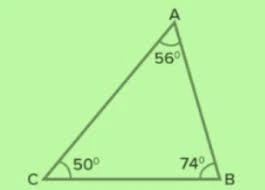
Example 1: Is the triangle shown in the figure above is acute scalene triangle?
Solution: Certainly! The triangle has three distinct side lengths and three acute angles.
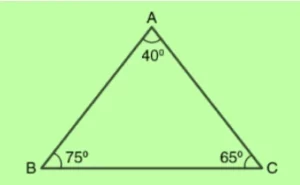
Example 2: Is this an acute scalene triangle?
Solution: Not at all. Lines AB and AC are at least two equal sides, even though all three angles are acute.