List of Perfect Squares

Answer: Perfect squares represent a distinct subset of numbers possessing several exceptional characteristics. Numerous factorization strategies that help decompose more complex mathematical problems are based on these features.

Perfect Squares: What Are They?

Perfect squares are numerical expressions that are expressed as the product of an integer and itself. The perfect square can also be expressed as an integer’s second exponent since it is simply the same number multiplied twice. Therefore, perfect squares are the squares of all numbers.

For example, 16 is a perfect square because it is the result of multiplying an integer by itself.

4×4 = 16

Furthermore, the product (-4) with (-4) gives 16.

The squares of 4 and -4 are the same.

Formula for Perfect Squares

Given that perfect squares are integers that can be written as the square of an integer multiplied by itself, we can use them to express any integer. One way to express the perfect squares formula is:

P = nxn = n2

where n is an integer and P is a perfect square number.

What Is a Perfect Square Number?

A number from the natural number set N that can be written as the product of another integer number and itself is known as a perfect square. An exponent of 2, sometimes referred to as an index or power, can be used to indicate the product of two equal integers when the integer number serves as the base number. The square root of the perfect square number is another name for this figure. The opposite of square rooting a number is square rooting a number. 

The following is the formal definition in mathematics:

If an is a perfect square integer such that n=a×a = a2 for all n in N, then n exists. We refer to the square root of n as the integer a. 

As the integer set Z is closed under multiplication, any number that is the product of two integers in Z must also be in Z. This is true since N is a subset of Z.

Characteristics of the Perfect Square

• The last number is either 1, 4, 5, 6, or 9.
• 1, 4, 7, 9, is always the digital root.
• The preceding digit needs to be odd if the last digit is 6.
• The preceding digit is even if the last digit is not six.
• The preceding digit must be 2 if the last digit is 5.
• The square root of an even number is also even. There is an odd square root for odd squares.
• The number of prime factors in them is always odd.
• One of two values results from dividing the remainder by 4.
• Either 1 or 0 is the remaining amount after dividing by 3.
• It must also finish with an even number of zeros if the final digit is zero.

How to Spot Perfect Squares?

The final digit of the integer is usually the most important factor to consider when identifying perfect squares.

Example1: The following are not perfect squares: 732, 2747, 3928, and 19253.

Example 2: 3857 = 3 + 8 + 5 + 7 = 23, 2 + 3 = 5 is its digital root. 3857 is therefore not a perfect square.

Even so, the presence of certain qualities in a number does not guarantee that it is a perfect square; rather, it suggests that it MAY be one. For instance, 22 is not a square number, yet its digital root is 4. Furthermore, the number is instantly ruled out as square because it ends in 2.

After locating a potential perfect square, you can carry out additional research by determining the square root of an integer. This is the primary way of finding a perfect square. It would follow that a number is a perfect square if its integer square root could be proven. It simply takes five steps to use the most efficient and straightforward procedure to discover a number’s square root! These are listed in the following order:

• As soon as you are given a number n, combine its final two digits into a pair. Keep the other numbers apart from each other.
• Keep in mind that the final digit of n can provide us with an estimate of the potential final digit of the square root of a. It is the square root of a perfect square expressed as a single digit with the same final digit. Two numbers are possible to you.
• After removing the pair, find the ideal square that is smaller than but still closest to the group formed by the integers. Observe its square root. This is a square root digit that will be positioned next to the final digit that was determined in the subsequent steps.
• Increase the square root multiplied by one beyond the square root obtained in step 3.
• You want to designate the smaller of the two numbers discovered in step 2 as the final digit of an if the number discovered in step 4 is greater than the number set. The greater of the two numbers in step 2 should be selected if it is smaller.

You can find the square root of an integer by combining your answers.

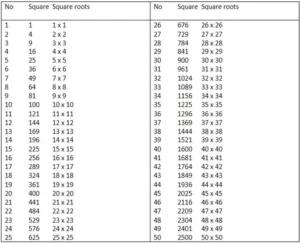
A List of Perfect Squares

An index of the first fifty integer square numbers is provided below: