Answer: The space that an object takes up in three dimensions is known as its volume. A volume of the square is the area that each of its five faces occupies. A three-dimensional geometric shape known as a square pyramid is made up of four triangular side faces connected to a square base, which meets at the pyramid’s peak.
What Is a Square Pyramid?
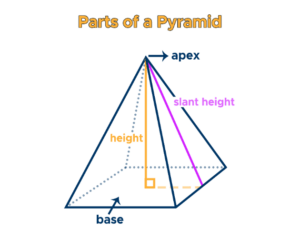
The term “square pyramid” refers to a three-dimensional object with a square base, five triangular faces, and a face attached to each of the square base’s sides. The faces are then closed together so that the vertex of the square pyramid is the point at which the tops of all the bases meet. A few examples of square pyramids are the Great Pyramid in Giza, ornamental objects, wine or perfume bottles, etc. A square pyramid is composed of three parts:
- The top of the square pyramid is known as the apex of the pyramid
- A Square Base
- Four Triangular Faces
What Is the Volume of a Square Pyramid?
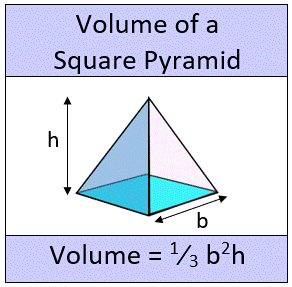
The area of the base multiplied by the pyramid’s height equals one-third of the volume of a square pyramid. Therefore, volume is equal to (1/3) × (Base Area) × (Height). The quantity of unit cubes that can fit inside a square pyramid is known as its volume, and it is expressed in “cubic units”. It is commonly stated as m3, cm3, in3, etc.
Three-dimensional, five-faced shapes are referred to as square pyramids. A square pyramid is a type of polyhedron, also known as a pentahedron that is made up of four triangles joined to a vertex and a square base. It has a square base and triangle side faces with a common vertex on each side.
Volume of a Square Pyramid: Formula
The height and base area of a square pyramid are all that are needed to quickly calculate its volume, which is as follows:
Volume of a square pyramid = (1/3) Base Area × Height
Let us now assume a standard square pyramid with side ‘b’ equilateral triangles.
A regular square pyramid’s volume can be calculated using the following formula:
Volume of a regular square pyramid = 1/3 × b2 × h
Where,
The square pyramid’s base side is denoted by b.
The square pyramid’s height is represented by h.
Steps To Determine the Volume of a Square Pyramid
As we discovered in the previous section, (1/3) Base Area × Height can be used to calculate the volume of a square pyramid. Thus, to get the volume of a square pyramid, we take the steps listed below.
Step 1: Take note of the pyramid’s measurements based on the provided data, such as its height and base area.
Step 2: Divide the base’s area by both (1/3) and height.
Step 3: Use cubic units to show the final solution.
Example Solutions on the Volume of a Square Pyramid
Example 1: A sanitizing container has a square pyramidal shape with a side length of 3 inches and a height of 9 inches. Calculate the amount of sanitizer that a bottle can carry using the volume of a square pyramid formula.
Solution: Given that
Base Area (A): 60 m2
Height (H): 10 m
Applying the Formula,
V = 1/3 × A × h.
V = 1/3 × 60 × 10
V is equivalent to 200 m3
As a result, the specified square pyramid has a volume of 200 m3.
Example 2: Calculate the volume when a pyramid’s height and base length are known.
Solution: Given the availability of all necessary variables, this is the easiest problem you will encounter. Directly enter the values of a and h into the formula.
V = ⅓ x 42 x 9 = 48 m3
where the unit of measurement is m3, which stands for cubic meters. The reason for this is that the square base’s area is 4 x 4 = 16 m^2, or 16 square meters. This figure is multiplied by the nine meters of height.
As a result, we get the product of three-meter values, or m x m x m = m3.
Example 3: A sanitizing container has a square pyramidal shape with a side length of 3 inches and a height of 9 inches. Calculate the amount of sanitizer that a bottle can carry using the volume of a square pyramid formula.
Solution: We are aware that the volume of a square pyramid with a side of a and a height of h is:
Square pyramid volume = 1/3 × a2 × h
When we transfer the values of a and h, we have
Square pyramid volume = 1/3 × a2 × h
1/3 × 32 × 9 = 27
Therefore, a sanitizing container has a volume of 27 inches3.
Other Types of Pyramids
- Rectangular Pyramid
A pyramid having a rectangular base is called a rectangle pyramid. All square pyramids are rectangular pyramids because squares are a kind of rectangle. However, the opposite is untrue.
- Triangular Pyramid
The term Tetrahedron refers to a triangle pyramid. This pyramid is triangular on all its faces. The volume can be calculated by applying the generalized formula.
- Oblique Pyramid
An oblique pyramid is one in which the square base’s midway is not exactly where the apex is located. The same method can be used to get the volume of an oblique pyramid, and the height of one is equal to the perpendicular distance between the base and the peak of the pyramid.